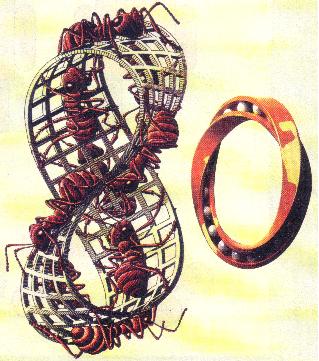Не слід  плутати  те , що нам зда­ється неймовірним і неприрод­ним, з абсолютно неможливим.

К. Ф.Гаусс

                                Август Фердінанд Мебіус

                           (1790-1868)

Відомий і таємничим лис­ток Мебіуса

(іноді кажуть:  стрічка Мебіуса)

винайшов 1858 року

німецький  геометр
Август  Фердінанд  Ме­біус,
учень «короля  матема­тиків»
Карла Гаусса.  
Мебіус  починав як астроном.
Того часу заняття

математикою не  знаходило належної
під­тримки, астрономія ж давала
достатньо коштів, щоб не думати про
них, і залиша­ла  вдосталь часу для власних роздумів. Мебіус став  одним із  найвидатніших   ге­ометрів  XIX ст. У віці   68 років він   зробив відкриття    неймовірної краси —   лис­ток Мебіуса.

ЩО ТАКЕ ЛИСТОК МЕБІУСА?

Візьмемо паперову стрічку АВСD і скле­їмо

кінці так, щоб точка А збіглася з точ­кою D,

а точка В — з точкою С (тобто перед 

склеюванням перекрутимо стрічку один раз).

Ми отримали видатне в математиці паперове

кільце — листок Мебіуса.

                   СКІЛЬКИ СТОРІН У ЛИСТКА МЕБІУСА?

Якщо на внутрішню сторону звичайного

кіль­ця   посадити муху, а на зовнішню — 

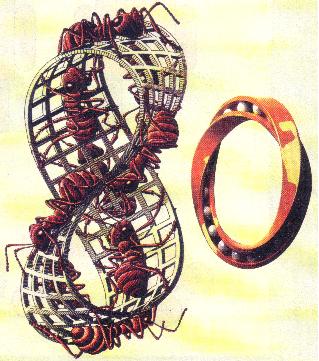
павука і дозволити  їм повзати

як завгодно, тільки  не переповзати

через  край, то павук ніколи не зможе

впіймати муху. А  якщо їх обох
 

посади­ти на листок Мебіуса, то павук

 з'їсть бідну му­ху (звичайно, якщо він

швидше бігає).
 

Візьмемо іграшкового солдатика і  

відправи­мо його у  подорож по лінії,

яку проведено на листку Мебіуса.

Через деякий час він   повер­неться до місця старту. Але в якому

положен­ні?  У перевернутому! Для того щоб він повер­нувся до старту у

звичайному  положенні, йому слід   здійснити ще одну

«навкололисткову» по­дорож.

             
 ЕКСПЕРИМЕНТИ ДЛЯ ВСІХ

1.Візьміть стрічку АВСD, розділіть її по ширині на дві однакові частини  пунктирною лінією (паралельною  сторонам  АС і ВD) і, перекрутивши один раз,  склейте листок Мебіуса. Розріжте його ножицями за

2.Розріжте кільце, одержане в першому експерименті, ще раз. Ви одержите два зціплених одне з одним кільця, причому кожне з них перекручене двічі.

3.Підготуйте два листки Мебіуса, попередньо розділивши стрічку лініями на  чотири і п'ять рівних смуг пунктирними лініями. Розріжте за цими лінія­ми. Що ви одержали? Чи можна висловити яке-небудь твердження щодо «по­ведінки»  листка Мебіуса під час відрізання від нього смужки? Що буде, якщо перед  склеюванням перевернути стрічку двічі, а потім розрізати вздовж посе­редині?

А якщо перед склеюванням перевернути стрічку тричі? Можна при­думати ще  багато експериментів із розрізанням стрічок. Якщо виникло бажання зробіть  це. Думайте, експериментуйте!       Наочність